Beweisen digital lernen – Vom Verstehen zur Konstruktion
Projektziel: Erstellung von digitalen Unterstützungsmöglichkeiten für das Verständnis und selbstständige Konstruieren von Beweisen in der Mathematik
Status: abgeschlossen

Vorhaben
Studiengänge mit einem hohen Mathematikanteil zeichnen sich durch eine hohe Abbruchquote aus. Eine der größten Hindernisse für die Studierenden ist das mathematische Beweisen – ein Hauptbestandteil vieler Mathematikveranstaltungen, der in der Schule aber häufig nur marginal behandelt wird.
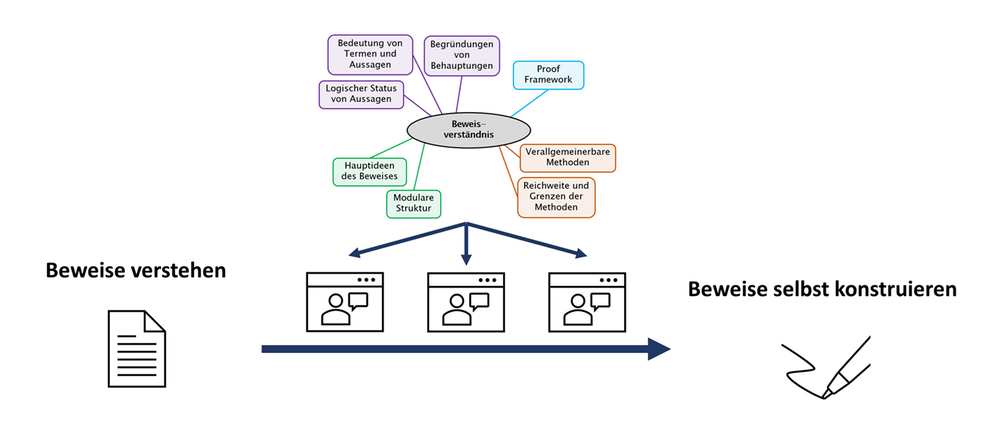
Das „Beweisen“ lässt sich in verschiedene Aktivitäten unterteilen: In den Lehrveranstaltungen und Lehrbüchern sind Beweise vorgegeben, die Studierende als Lerngelegenheit nutzen können. Dazu müssen sie diese zunächst verstehen und nachvollziehen, um damit ihr Wissen über Mathematik zu vertiefen. Daneben sollen Studierende auch selbst Beweise konstruieren und ggf. auch präsentieren. Eine Vermutung ist dabei, dass Studierende lernen, Beweise selbst zu konstruieren, indem sie vorgegebene Beweise nachvollziehen.
Um diesen Lernprozess zu unterstützen, werden im Teilprojekt digitale Zusatzangebote entwickelt, mit denen Studierende die Prozesse und Strategien beim Beweisen (vor allem das Verstehen und Konstruieren) eigenständig erlernen und üben können. Die Umsetzung soll aktive Interaktion von den Studierenden verlangen und prozessbegleitend evaluiert werden.
Auch allgemeine Erkenntnisse, inwiefern mithilfe von digitalen Medien Lernstrategien gelehrt und solche Unterstützungsmöglichkeiten digital umgesetzt werden können, sind Ziele des Projekts in Hinblick auf die Lehramtsausbildung. Dabei wird von Beginn an darauf geachtet, die Angebote möglichst studiengangsübergreifend (z. B. zwischen Lehramt Mathematik und B.Sc. Mathematik) und somit für verschiedene Veranstaltungen nutzbar zu konzipieren.
Durch das studienbegleitend verfügbare digitale Unterstützungsangebot sollen Kompetenzerlebnisse direkt zu Studienbeginn ermöglicht werden. Das Angebot soll zudem eigenständig und zeit- bzw. ortsunabhängig bearbeitbar sein und so das Autonomieerleben der Studierenden unterstützen.
Die Einbindung kann in Vorkursen oder parallel zu den Vorlesungen zu Beginn des Studiums erfolgen und dient damit auch einer Entlastung der Dozierenden, die somit eher den spezifischen Inhalt ihrer Veranstaltung fokussieren können.
Wichtig ist, dass nicht nur passiv konsumierbare Angebote wie Lernvideos konstruiert werden, sondern durch interaktive Inhalte eine Aktivierung der Studierenden erfolgt. Dadurch soll ein tiefergehendes und nachhaltiges Lernen ermöglicht werden (deeper learning).
Es profitieren alle Studiengänge mit einem hohen Mathematikanteil (Lehramtsstudium Mathematik, Mathematik, etc.) von dem Vorhaben.
Das Projekt wird von der Didaktik der Mathematik (Bereich Hochschuldidaktik) durchgeführt.
Deci, E. L. & Ryan, R. M. (1993) Die Selbstbestimmungstheorie der Motivation und ihre Bedeutung für die Paedagogik. Zeitschrift für Pädagogik, 39(2), 223-238.
Heintz, B. (2000). Die Innenwelt der Mathematik: Zur Kultur und Praxis einer beweisenden Disziplin. Springer Verlag.
Neuhaus-Eckhardt, S. (2022) Beweisverständnis von Studierenden – Zusammenhänge zu individuellen Merkmalen und der Nutzung von Beweislesestrategien. Waxmann.
Neuhaus-Eckhardt, S. & Rach, S. (2023). Constructing a proof after comprehending a similar proof – relation and examples. In M. Ayalon, B. Koichu, R. Leikin, L. Rubel & M. Tabach (Hrsg.). Proceedings of the 46th Conference of the International Group for the Psychology of Mathematics Education (Vol. 3, S. 403-410). PME.
Rav, Y. (1999). Why do we prove theorems? Philosophia mathematica, 7(1), 5–41.
Rodríguez, L. & Cano, F. (2006). The epistemological beliefs, learning approaches and study orchestrations of university students. Studies in Higher Education, 31(5), 617–636.
Es werden zunächst vor allem Lernvideos mit eingebundenen H5P-Elementen erstellt, die eine aktive Nutzung ermöglichen und durch die die Studierenden gleichzeitig erstes Feedback erhalten können.